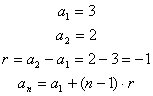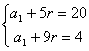Ciąg arytmetyczny

Definicja:

Ciąg liczbowy () nazywamy ciągiem arytmetycznym, jeżeli istnieje taka liczba r, że każdy następny wyraz ciągu oprócz pierwszego powstaje przez dodanie tej liczby do wyrazu poprzedniego:

.

dla każdej liczby N. Liczbę  nazywamy różnicą ciągu.

Dla ciągu arytmetycznego o pierwszym wyrazie  i różnicy  wzór ogólny ciągu ma postać:

.

Ciąg arytmetyczny () jest rosnący, gdy ; malejący, gdy  oraz stały, gdy .

Jeżeli () jest ciągiem arytmetycznym, to dla  wyraz n-ty jest średnią arytmetyczną wyrazów z nim sąsiadujących:

.

Przykład 1.

Znajdź różnicę i oblicz dwudziesty wyraz ciągu arytmetycznego:  3, 2, 1, 0, -1, -2,…..

Rozwiązanie

Zadanie 1.

Oblicz trzydziesty wyraz ciągu arytmetycznego:  a)  2, 4, 6, 8, 10…….

b)      1, 11, 21, 31, 41,…….

Odpowiedzi:  a)  60

b)      291

Przykład 2

Wykaż, że ciąg   jest ciągiem  arytmetycznym.

Należy wykazać, że różnica   jest stała dla każdej liczby .

Badamy różnicę 

Stąd wynika, że ciąg jest arytmetyczny.

Zadanie 2.

Wykaż, że ciąg   jest arytmetyczny :  a)  

                                                                    b)  

                                                                    c)  

Przykład 3

Wyznacz   i  r   oraz podaj wzór ogólny ciągu arytmetycznego jeżeli    

Rozwiązanie

Korzystając ze wzoru   otrzymujemy:  

Rozwiązujemy układ równań:  

Otrzymujemy:  

Wyznaczamy wzór ogólny ciągu  podstawiając obliczone dane do wzoru

Otrzymujemy:  

Zadanie  3.

Wyznacz   i  r   oraz podaj wzór ogólny ciągu arytmetycznego jeżeli :

a)  

b)  

c)  

Odpowiedzi:    a)  

                         b)  

                         c)
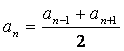