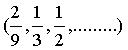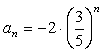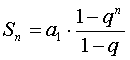Ciąg geometryczny

Ciąg liczbowy  nazywamy ciągiem geometrycznym, jeżeli istnieje taka liczba q , że każdy wyraz ciągu, oprócz pierwszego, powstaje przez pomnożenie wyrazu poprzedniego przez tę liczbę:

dla każdej liczby naturalnej  .

Liczbę q nazywamy ilorazem ciągu.

Zadanie 1.

Wypisz cztery pierwsze wyrazy ciągu geometrycznego jeżeli:

a) 

Rozwiązanie

b) 

c)  

Jeżeli  jest ciągiem geometrycznym , to:

Zadanie 2.

Wyznacz    ciągu geometrycznego jeżeli:

a)  

Rozwiązanie

b)  

c)  

Zadanie 3.

Oblicz siódmy wyraz ciągu geometrycznego jeżeli:

a)         ( 1, 3, 9, 27,………)

Rozwiązanie

b)        (3, 6, 12, 24,………)

c)        

Ciąg  , o wyrazach różnych od zera , jest ciągiem geometrycznym , jeśli dla dowolnego   iloraz   jest stały.

Zadanie 4.

Sprawdź na podstawie definicji czy ciąg  jest geometryczny.

a) 

Rozwiązanie

Ciąg  jest geometryczny , ponieważ iloraz jest stały.

b) 

c)  

d)  

Jeśli  jest ciągiem geometrycznym o ilorazie    , to suma n początkowych wyrazów tego ciągu  jest równa:

Zadanie  5.

Oblicz sumę dziesięciu początkowych wyrazów ciągu geometrycznego:

a)      ( 3, 9, 27, 81,…….)

Rozwiązanie

b) 

c)  

Zadania utrwalające

Zadanie 1

Znajdź iloraz ciągu geometrycznego , w którym:

a)                 b)         c)   

Odp:   a)        b)          c) 

Zadanie 2

Znajdź piąty wyraz ciągu geometrycznego   

Odp:    

Zadanie 3

Znajdź sumę n początkowych wyrazów ciągu geometrycznego  jeżeli:

 a)  

b)   

Odp:   a)                       b)  

Zadanie  4

Znajdź pierwszy wyraz ciągu geometrycznego , w którym:

a)         b)  

Odp:   a)      b) 

Zadanie  5

Liczby   -2, x, y, z, -32  w podanej kolejności tworzą ciąg geometryczny. Znajdź x, y, z.

Odp:   ( 4, -8, 16 )      ( -4, -8, -16 )

Zadanie  6

Zbadaj czy ciąg     jest geometryczny.

Zadanie  7

Podaj wzór ogólny ciągu geometrycznego  jeżeli  

Odp: