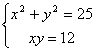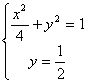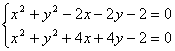Układy równań kwadratowych

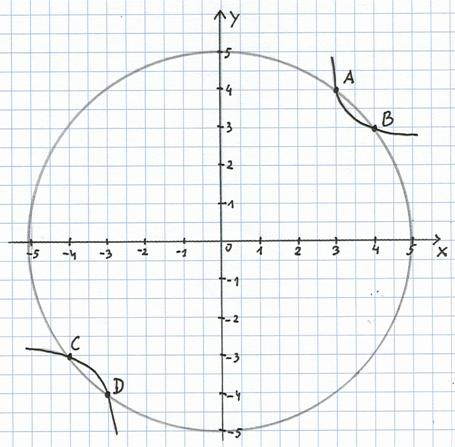
 Przykład 1.

Pierwsze równanie przedstawia okrąg  o środku w punkcie S = ( 0, 0 ) i promieniu r = 5.

Drugie równanie przedstawia hiperbolę.

Graficzne rozwiązanie układu  przedstawia rysunek nr 1. Układ ma zatem cztery rozwiązania: A = ( 3; 4 ) ,  B = ( 4; 3 ) ,  C = ( -4; -3 ) ,  D = ( -3; -4 )

 Rozwiąż układ algebraicznie.

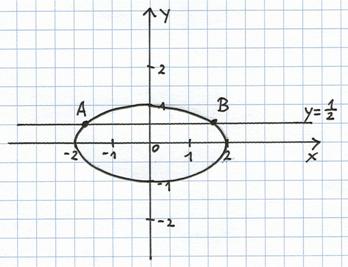
Rys.1

Przykład 2.

Równanie   przedstawia elipsę , zaś równanie   przedstawia prostą równoległą do osi OX.

Na rysunku nr 2 przedstawiono geometryczną interpretację rozwiązania układu równań .

Krzywe zadane powyższymi równaniami przecinają się w dwóch punktach. Układ równań ma dwa rozwiązania :        

Rozwiąż układ algebraicznie.

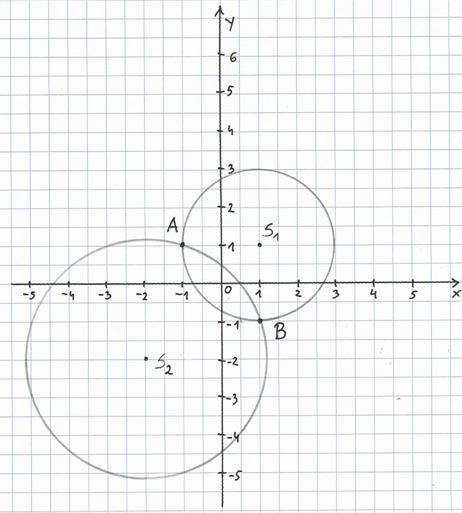
Rys.2

Przykład 3.

 Równania tworzące układ równań przedstawiają okręgi.

Pierwsze równanie przedstawia okrąg o środku w punkcie   i promieniu  .

Drugie równanie przedstawia okrąg o środku w punkcie   i promieniu 

Rysunek nr 3 przedstawia wzajemne położenie tych okręgów w układzie współ rzędnych. Okręgi te przecinają się w dwóch punktach  A = ( -1; 1 )  i B = ( 1; - 1 ).  Stąd wynika, że układ równań ma dwa rozwiązania.

Rozwiąż układ algebraicznie.

Rys.3